AliasMethod是一个初始化复杂度为O(n),占用内存O(n),运行时复杂度为O(1)的算法。
核心文献:http://www.keithschwarz.com/darts-dice-coins/
本文部分文字来自上文翻译。
AliasMethod使用场景
这里用游戏服务来举例,当我们打开一个宝箱会随机获得一件宝物,宝物可能出现的概率如下:
青龙偃月刀 15%
丈八蛇矛 15%
龙胆亮银枪 15%
青釭剑 20%
卷云刀 35%
一般做法:我们将其概率相加等于100,意思是将其看成有100份分片,第0-14片表示青龙偃月刀,第15-29片表示丈八蛇矛……,然后利用rand()%100获得第几片,代表获得了第几件宝物,显然这种做法的运行时获取结果的时间复杂度为O(n)。
好一些的做法:我们将每样宝物的概率利用平衡二叉树构建初始化,如下图所示,利用二叉树的特性找到rand()%100结果对于所处树的节点,运行时获取结果的时间复杂度为O(log(N))。
AliasMethod的做法
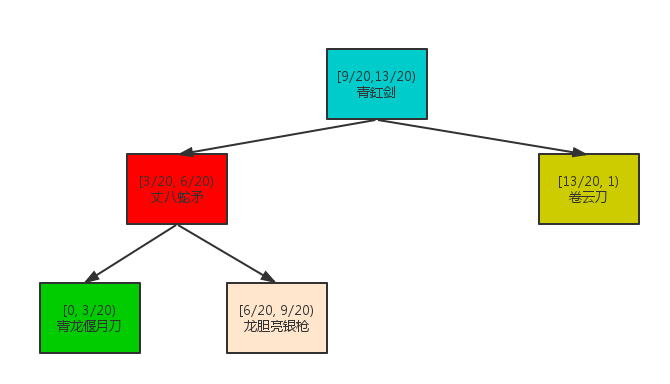
首先,我们将宝箱里宝物出现的概率抽象成下图:
简单来说这是一个概率占用空间的比例图,现在宝箱里有5件宝物,每件宝物的平均概率为20%,我可以明显的看到青龙偃月刀,丈八蛇矛,龙胆亮银枪是低于平均概率的,而卷云刀高于平均概率,因此将低于平均概率的宝物放入Small堆,将高于平均概率的宝物放入Large堆。

AliasMethod的核心思想就是将高于平均概率的宝物当做“别名”分配到低于平均概率宝物之上,做法大致步骤:
1、从Large堆里找到第一个元素,将其填充至Small堆第一个元素
2、若未填满,则从Large堆里找到下一个元素;若填满,则从Small堆找到下一个元素填充,这样循环下去
3、Large堆或者Small堆任何堆为空则退出循环
初始化分配后如图(概率后面是高度占比,区间(0,1]):
接下的来处理方式就比较简单了,我们随机取一个下标[0,4],比如下标2,对应的是宝物龙胆亮银枪(占比0.75),被分配的宝物为卷云刀(占比0.25),那么我们再从[0,1]随机一个浮点数,看落在龙胆亮银枪占比区间,还是落在卷云刀占比区间,落入对应区间获得相应宝物。
AliasMethod的误差(主要基于核心文献翻译)
当我们在理想情况下,通过概率计算出的权重是可以均分的。但是在复杂的情况下,特别是1/n会有小数余数的时候(例如 1/3=0.333333…..),使用double计算时就会存在精度问题。直接导致的结果使Small堆还存在元素,但是Large堆已分配空的情况(反之亦然)。
这里原文的解决方法是,无论是Small堆还是Large堆,在循环分配后,若还存在未分配的元素,那么我们强行将其占比置1。
这里笔者提一句,原文没有给出严格的数学证明上述做法是否会导致结果失真,但是从实际测试用例来看,误差在合理的范围之内。
使用C++实现的代码 – 请点这里
(全文结束)
转载文章请注明出处:漫漫路 - lanindex.com